| Section |
Information |
| Statistics: |
Original Name: AS145
Original Author: Marcia & Robert Ascher
Museum: Museum für Völkerkunde,
Museum Number: VA42533
Provenance: Pachacamac
Region: Unknown
|
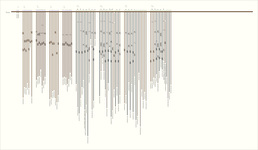
# of Cords: 90 (88p, 2s)
# of Unique Cord Colors: 4
Benford Match: 0.8554
# Ascher Sums (pps, ips, cps, sps,...): 26 (19, 5, 2, 0,...)
Similar Khipu: Previous (UR1144) Next (UR1130)
|
|
| UR1145/KH0161 |
 |
| Pendant Pendant Sum |

 |
| Indexed Pendant Sum |

 |
| Colored Pendant Sum |

 |
| DataFile: |
UR1145
|
| Notes: |
Ascher Databook Notes:
- A pendant fragment stored with the khipu was assumed to be part of pendant 37. Pendant 37 is broken at 16.0 cm.
- A pendant fragment stored with the khipu was assumed to be part of subsidiary 84s1 The subsidiary is broken at 10.5 cm.
- This is one of several khipus acquired by the Museum in 1907 with provenance Pachacamac. For a list of them, see UR1097.
- By spacing and color patterning, the khipu is separated in to 3 parts. The first part is one pair of pendants; the second is 4 groups of 7 pendants each; and the last part is 4 groups of 14 or 16 pendants each.
- The khipu has 2 different knot cluster arrangements. One is the standard arrangement involving single knot clusters and long knot clusters. The other arrangement is only long knot clusters in one or more of 3 distinct positions on a cord. For convenience, call the former S and the latter N. The S and N arrangements are alternated on the khipu. In part 2, pendants in groups 1 and 3 are all N while in groups 2 and 4, they are all S. In part 3, within each group, the pendants alternate N, S, N, S, etc. The color patterning reinforces the alternation: in part 2, in groups 1 and 3, all pendants are B and in groups 2 and 4, they are DB; in part 3, in the first 2 groups, the colors alternate LC, DB-W, and in the next 2 groups, they alternate LC or B, DB-W. Thus, the knot arrangements and colors alternate together so that the N arrangement is associated with B or LC and the S arrangement with DB or DB-W.
- Some of the values on the pendants in groups 1 and 3 of part 2 sum to each other. Two relationships are repeated for pendants 3 positions apart. Namely:
P3i + P3,i+1 = P1i for i=(1,4)
P3i + P1i = 2 P3,i-1 for i=(4,7)
|
| Bibliography: |
Bibliography for UR1145/KH0161:
| Year |
Author |
Title |
Pages |
| 1978 |
Ascher, Marcia, and Robert Ascher. |
Code of the Quipu: Databook. University Microfilms, Ann Arbor. |
680; 930-935 |
| 1981 |
Ascher, Marcia, and Robert Ascher. |
Code of the Quipu: A Study in Media, Mathematics, and Culture. University of Michigan Press, Ann Arbor. |
122-123 (ex.6.7) |
| 1986 |
Ascher, Marcia. |
Mathematical Ideas of the Incas.’ In Native American Mathematics, edited by Michael P. Closs, pp. 261–289. University of Texas Press, Austin. |
283 |
| 2005 |
Ascher, Marcia. |
How Can Spin, Ply, and Knot Direction Contribute to Understanding the Quipu Code? Latin American Antiquity 16(1):99–111. |
110 |
| 2006 |
Pereyra Sánchez, Hugo. |
Descripción de los quipus del Museo de Sitio de Pachacamac. Consejo Nacional de Ciencia, Tecnología e Innovación Tecnológica, Lima. |
14 |
| 1994 |
Urton, Gary. |
New Twist in an Old Yarn: Variation in Knot Directionality in the Inka Khipus. Baessler-Archiv Neue Folge 42:271-305. |
296 |
| 2014 |
Urton, Gary. |
Quipus de Pachamac. Ministerio de Cultura, Lima. |
43 |
| 2017 |
Urton, Gary. |
Inka History in Knots: Reading Khipus as Primary Sources. University of Texas Press, Austin. |
123; 261 |
|






