KH0105/AS092 - Colored Pendant Sums


Drawings:
Overview Detail View
All Khipus' Ascher Sum FieldmarksRight-Handed XRay
All Colored Pendant Sum RelationshipsLeft-Handed XRay
This Khipu's Fieldmark CatalogRight-Handed Sum Detail
This Khipu's DrawingLeft-Handed Sum Detail

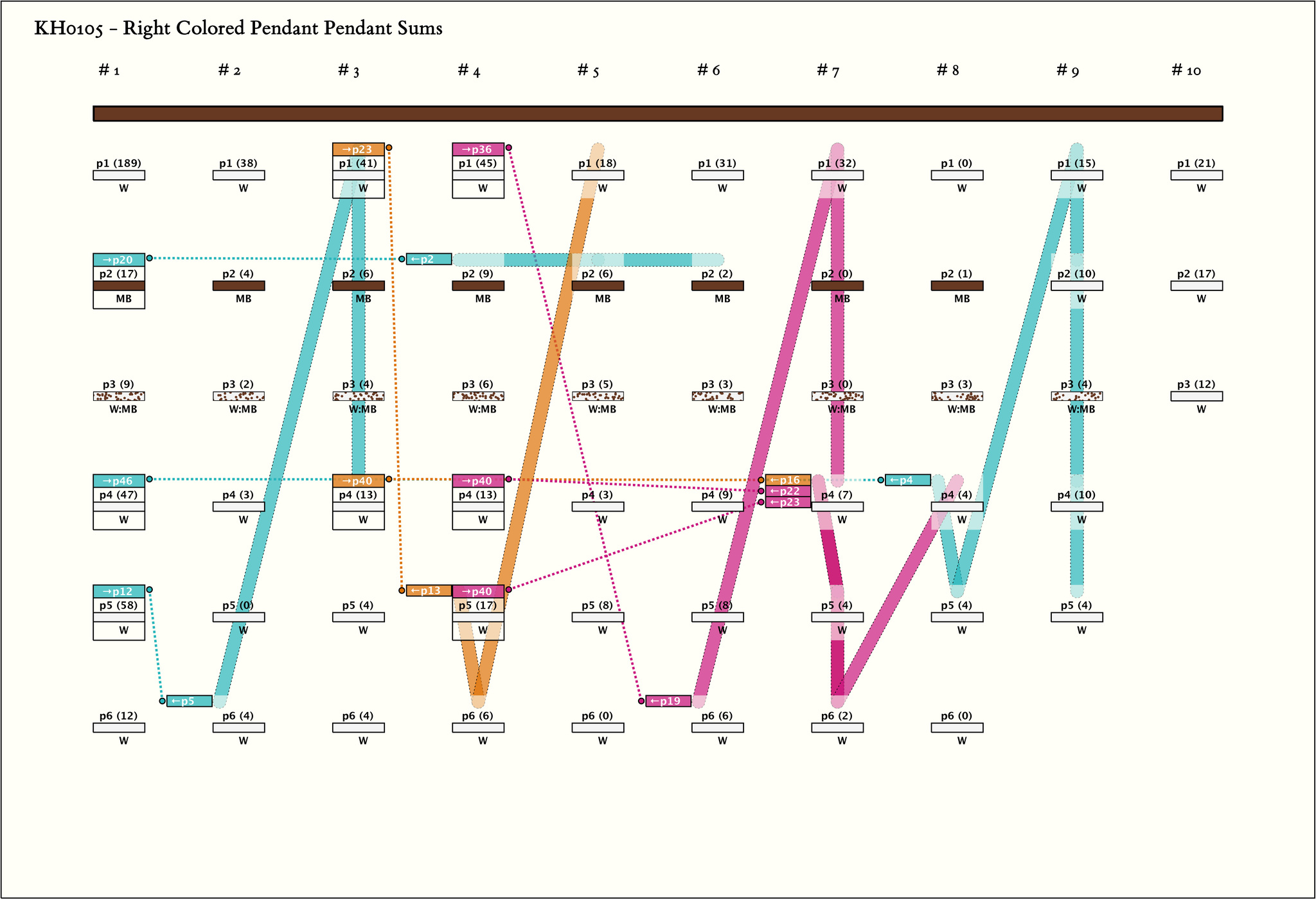
Right Handed Sums:     # Sums = 8,  Max # Summands = 6,   (Min, Mean, Max) Sum Values = (13, 31, 58)
Click on Image to View Larger

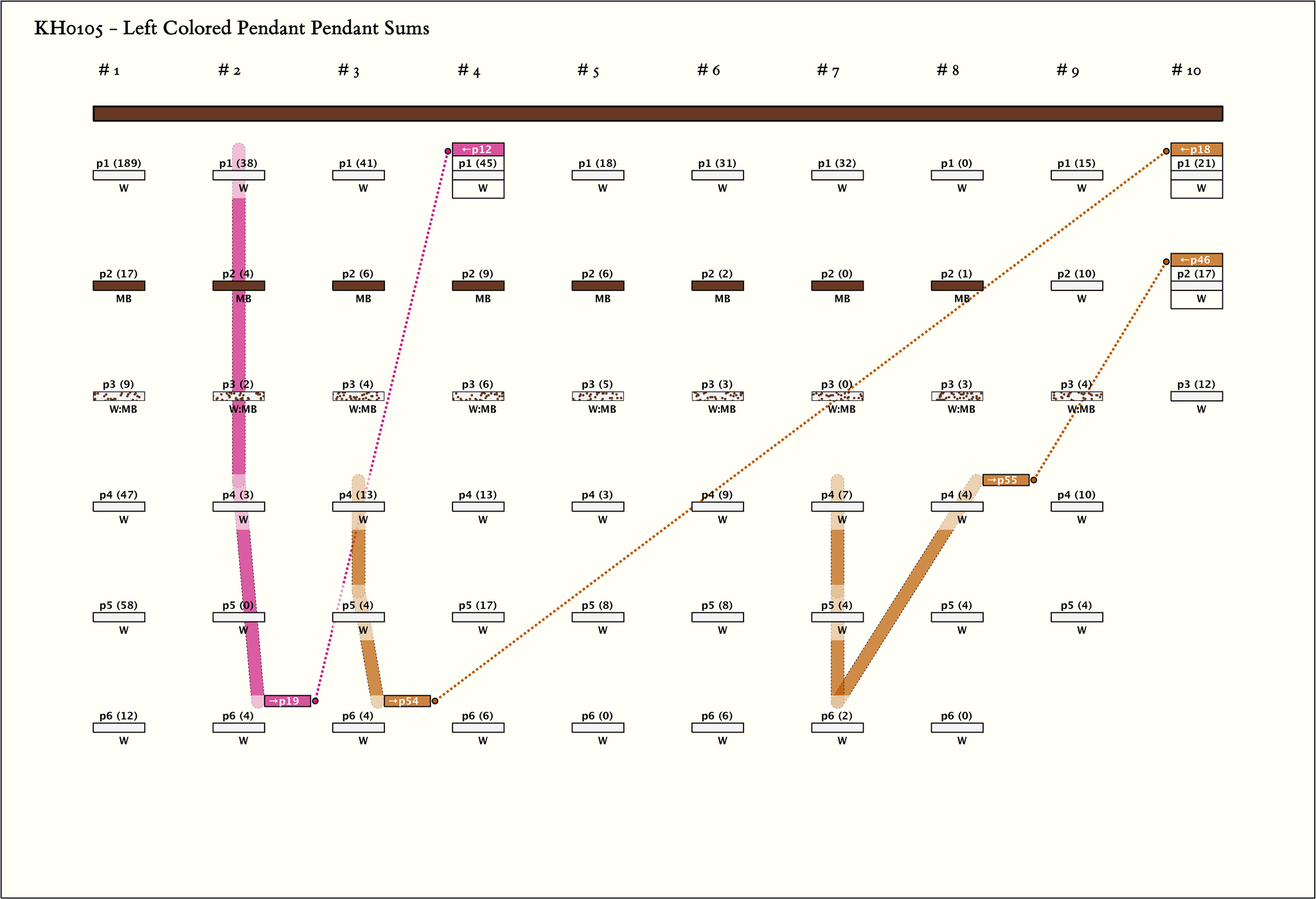
Left Handed Sums:     # Sums = 3,  Max # Summands = 4,   (Min, Mean, Max) Sum Values = (17, 28, 45)
Click on Image to View Larger

Right Handed Sum Detail: - Click on column name to sort
# Color Sum Schema Sum Cord Sum Cord Value # Summands Summands
1
g1p2 : 17MB173g4p2: 9MB + g5p2: 6MB + g6p2: 2MB
2
g1p4 : 47W476g8p4: 4W + g8p5: 4W + g9p1: 15W + g9p2: 10W + g9p4: 10W + g9p5: 4W
3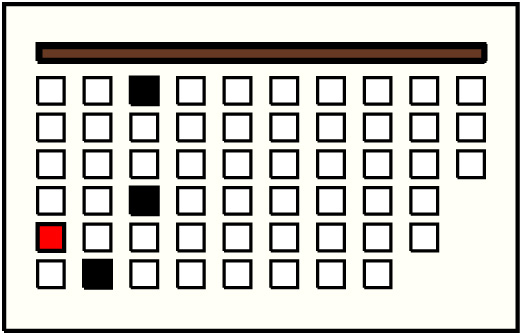
g1p5 : 58W583g2p6: 4W + g3p1: 41W + g3p4: 13W
4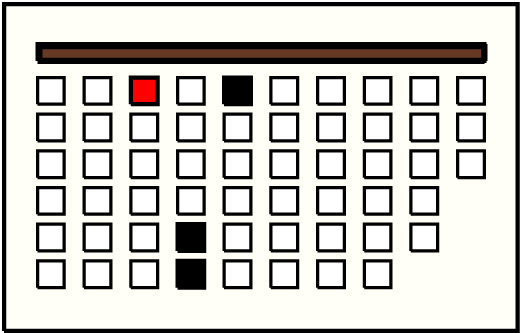
g3p1 : 41W413g4p5: 17W + g4p6: 6W + g5p1: 18W
5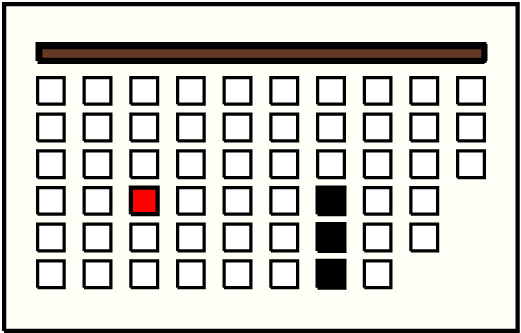
g3p4 : 13W133g7p4: 7W + g7p5: 4W + g7p6: 2W
6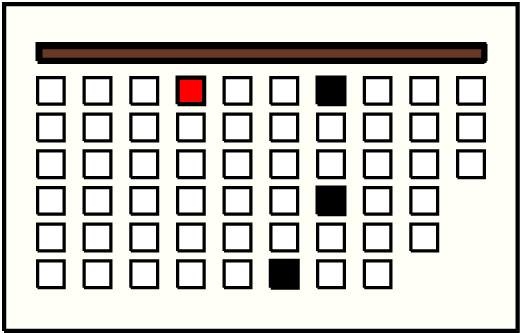
g4p1 : 45W453g6p6: 6W + g7p1: 32W + g7p4: 7W
7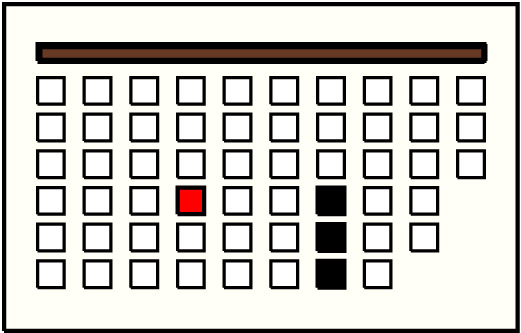
g4p4 : 13W133g7p4: 7W + g7p5: 4W + g7p6: 2W
8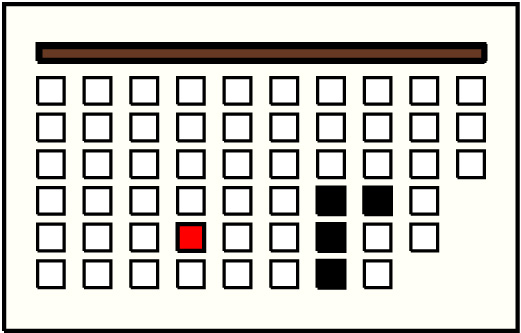
g4p5 : 17W174g7p4: 7W + g7p5: 4W + g7p6: 2W + g8p4: 4W

Left Handed Sum Detail: - Click on column name to sort
# Color Sum Schema Sum Cord Sum Cord Value # Summands Summands
1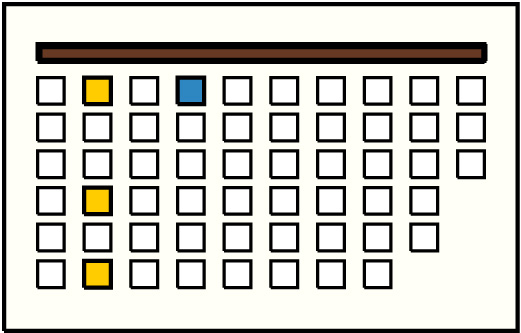
g4p1 : 45W453g2p1: 38W + g2p4: 3W + g2p6: 4W
2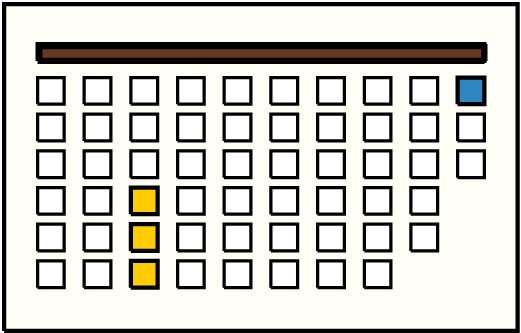
g10p1 : 21W213g3p4: 13W + g3p5: 4W + g3p6: 4W
3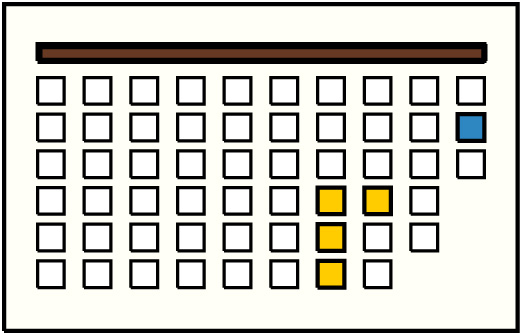
g10p2 : 17W174g7p4: 7W + g7p5: 4W + g7p6: 2W + g8p4: 4W

Khipu Notes:
Ascher Databook Notes:
  1. KH0100, KH0102, KH0103, KH0105, KH0106, KH0107 are associates in that the Museum designates them all as donated by Gaffron, and gives the provenance as Peru. For a comparison of them, see KH0100.
  2. By spacing, KH0105 is separated into 10 groups. The first 8 groups each have 6 pendants with the same color pattern (W, MB, MB:W, W, W, W).
  3. In all 10 groups, the first pendant has the maximum value.
  4. Position by position, the pendant values in group 1 are larger than those in group 4, which are larger than those in group 3, which are larger than those in group 2. That is:
    \[ P_{1i} > P_{4i} > P_{3i} > P_{2i}\;for\;\;i\;=\;(2,3,4,...,8) \]
  5. In a few cases, the sums of values in the same position in pairs of consecutive groups are equal. Namely:
    \[ P_{4i} + P_{5i} = P_{6i} + P_{7i}\;for\;\;i\;=\;(1,4) \]
    \[ P_{2i} + P_{3i} = P_{6i} + P_{7i}\;for\;\;i\;=\;(4,6) \]