KH0134/UR1120, AS120 - Colored Pendant Sums
Drawings:
Right Handed Sums: # Sums = 5, Max # Summands = 3, (Min, Mean, Max) Sum Values = (1068, 23675, 43372)
Click on Image to View Larger
Right Handed Sum Detail: - Click on column name to sort
| # | Color | Sum Schema | Sum Cord | Sum Cord Value | # Summands | Summands |
|---|---|---|---|---|---|---|
| 1 |  | g1p1 : 25691GG | 25691 | 3 | g2p1: 8731GG + g3p1: 11730GG + g4p1: 5230GG | |
| 2 |  | g1p2 : 1068B:LB | 1068 | 3 | g2p2: 362B:LB + g3p2: 457B:LB + g4p2: 249B:LB | |
| 3 |  | g1p3 : 42760LB | 42760 | 3 | g2p3: 14743LB + g3p3: 18053LB + g4p3: 9964LB | |
| 4 | 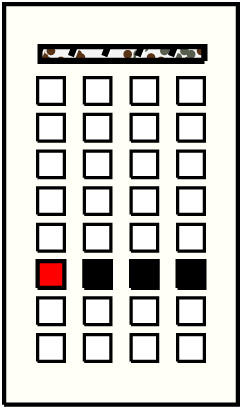 | g1p6 : 5485B-GG | 5485 | 3 | g2p6: 1862B-GG + g3p6: 2330B-GG + g4p6: 1293B-GG | |
| 5 | 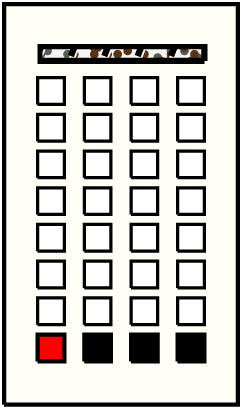 | g1p8 : 43372W:GG | 43372 | 3 | g2p8: 14701W:GG + g3p8: 18475W:GG + g4p8: 10196W:GG |
Khipu Notes:
Ascher Databook Notes:
- This is one of several khipus acquired by the Museum in 1907 with provenance Ica. For a list of them, see KH00110.
- By spacing, the khipu is separated into 4 groups of 8 pendants each. The color pattern for each group is the same (with the minor exception that pendants 7 and 8 in group 4 are B:GG and B/B-GG rather than the B-GG and B/B:GG of similar positions). In each group, there is one subsidiary on position 3 and it is the color of the pendant to which it is attached.
- The values in group 1 are the sums of the values of groups 2-4, position by position (with a discrepancy of 1 in the 4th position). The value on the subsidiary on position 3 in group 1 is also the sum of the values of the subsidiaries on position 3 in groups 2-4. Thus:
\[ \sum\limits_{i=2}^4 P_{ij} = P_{1j}\;\;\;\;\;for\;\;j=(1,2,...,8) \] - The ratios of the corresponding values is surprisingly consistent. For j =2,..., 8 and the position 3 subsidiary value:
p2j/P1j = 0.342 max. deviation 1.2%
p3j/P1j = 0.425 max. deviation 0.7%
p4j/P1j = 0.235 max. deviation 0.9%
The values on the exceptional position ( i=1) in the different groups, counterbalance each other. If 796 were subtracted from position 1 in group 3 and added to position 1 in group 4, the values in position 1 would also satisfy the above ratios.