UR1120/KH0134 - Colored Pendant Sums
Drawings:
Right Handed Sums: # Sums = 5, Max # Summands = 3, (Min, Mean, Max) Sum Values = (1068, 23675, 43372)
Click on Image to View Larger
Right Handed Sum Detail: - Click on column name to sort
| # | Color | Sum Schema | Sum Cord | Sum Cord Value | # Summands | Summands |
|---|---|---|---|---|---|---|
| 1 |  | p11, 1 : 25691GG | 25691 | 3 | p9: 8731GG + p17: 11730GG + p25: 5230GG | |
| 2 |  | p21, 2 : 1068B:LB | 1068 | 3 | p10: 362B:LB + p18: 457B:LB + p26: 249B:LB | |
| 3 |  | p31, 3 : 42760LB | 42760 | 3 | p11: 14743LB + p19: 18053LB + p27: 9964LB | |
| 4 | 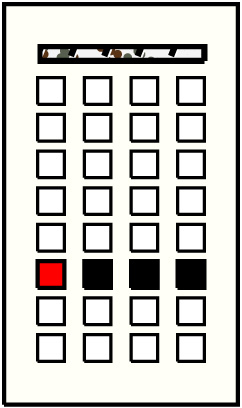 | p61, 6 : 5485B-GG | 5485 | 3 | p14: 1862B-GG + p22: 2330B-GG + p30: 1293B-GG | |
| 5 | 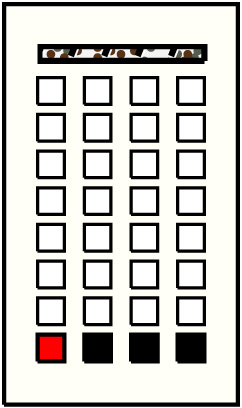 | p81, 8 : 43372W:GG | 43372 | 3 | p16: 14701W:GG + p24: 18475W:GG + p32: 10196W:GG |
Khipu Notes:
Ascher Databook Notes:
- This is one of several khipus acquired by the Museum in 1907 with provenance Ica. For a list of them, see UR1100.
- By spacing, the khipu is separated into 4 groups of 8 pendants each. The color pattern for each group is the same (with the minor exception that pendants 7 and 8 in group 4 are B:GG and B/B-GG rather than the B-GG and B/B:GG of similar positions). In each group, there is one subsidiary on position 3 and it is the color of the pendant to which it is attached.
- The values in group 1 are the sums of the values of groups 2-4, position by position (with a discrepancy of 1 in the 4th position). The value on the subsidiary on position 3 in group 1 is also the sum of the values of the subsidiaries on position 3 in groups 2-4. Thus:
\[ \sum\limits_{i=2}^4 P_{ij} = P_{1j}\;\;\;\;\;for\;\;j=(1,2,...,8) \] - The ratios of the corresponding values is surprisingly consistent. For j =2,..., 8 and the position 3 subsidiary value:
p2j/P1j = 0.342 max. deviation 1.2%
p3j/P1j = 0.425 max. deviation 0.7%
p4j/P1j = 0.235 max. deviation 0.9%
The values on the exceptional position ( i=1) in the different groups, counterbalance each other. If 796 were subtracted from position 1 in group 3 and added to position 1 in group 4, the values in position 1 would also satisfy the above ratios.