AS050/KH0061 - Indexed Pendant Sums


Drawings:
Overview Detail View
All Khipus' Ascher Sum FieldmarksRight-Handed XRay
All Indexed Pendant Sum RelationshipsLeft-Handed XRay
This Khipu's Fieldmark CatalogRight-Handed Sum Detail
This Khipu's DrawingKhipu Notes

Right Handed Sums:     # Sums = 3,  Max # Summands = 3,   (Min, Mean, Max) Sum Values = (12, 32, 56)
Click on Image to View Larger

Left Handed Sums:     # Sums = 0,  Max # Summands = nan,   (Min, Mean, Max) Sum Values = (nan, nan, nan)
Click on Image to View Larger

Right Handed Sum Detail: - Click on column name to sort
# Color Sum Schema Sum Cord Sum Cord Value # Summands Summands
1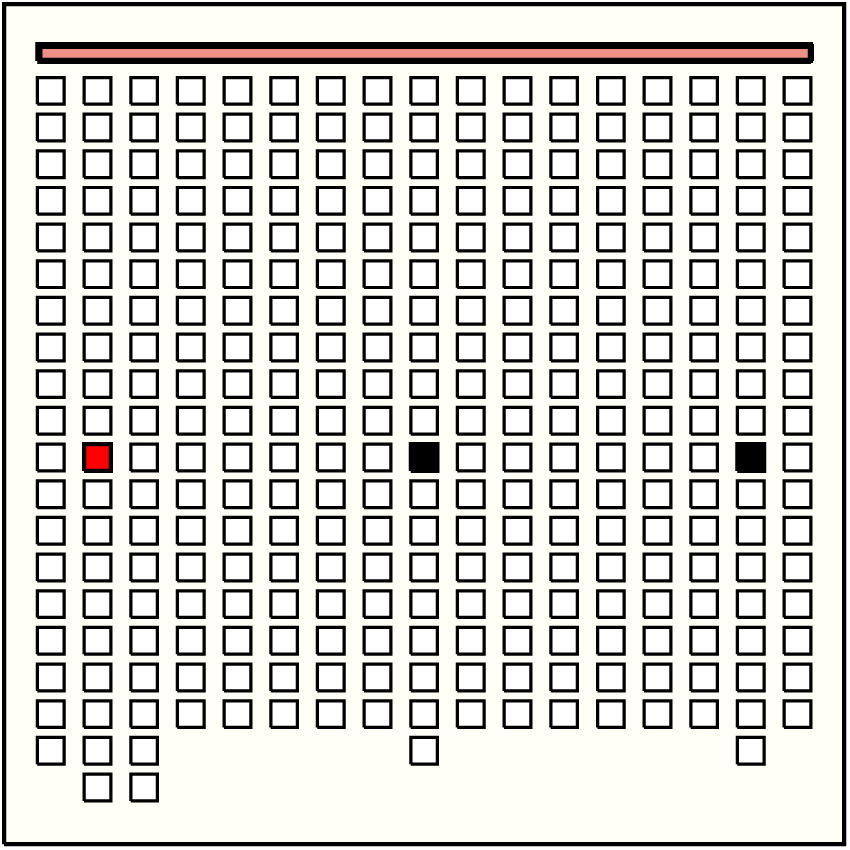
p302, 11 : 56B562p160: 29B + p287: 27B
2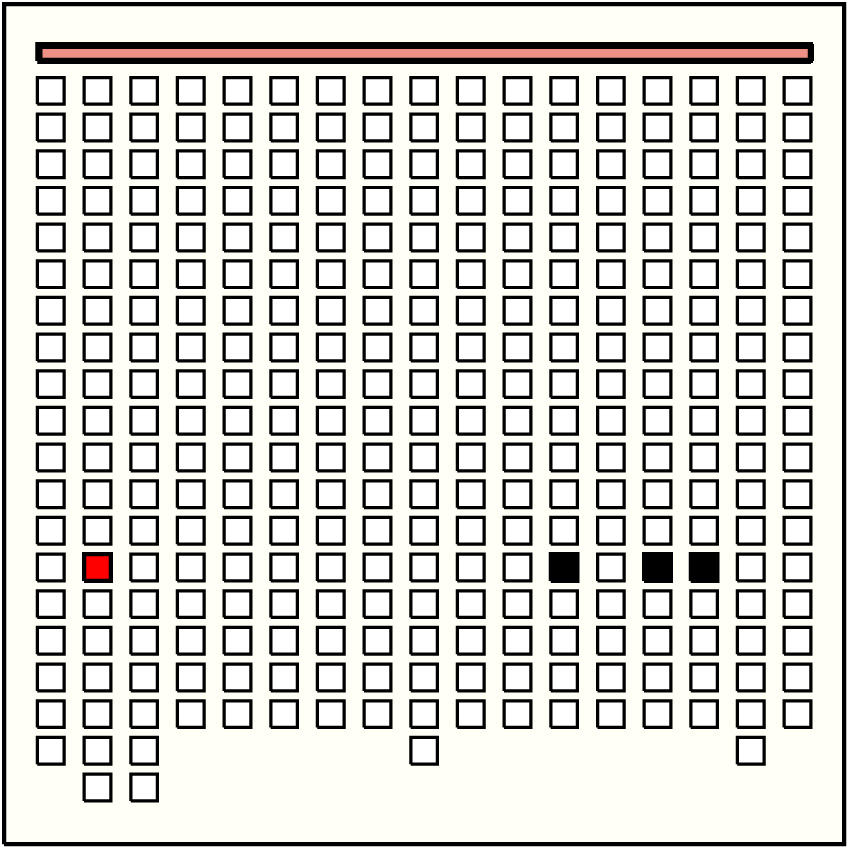
p332, 14 : 27BD273p218: 10BD + p254: 11BD + p272: 6BD
3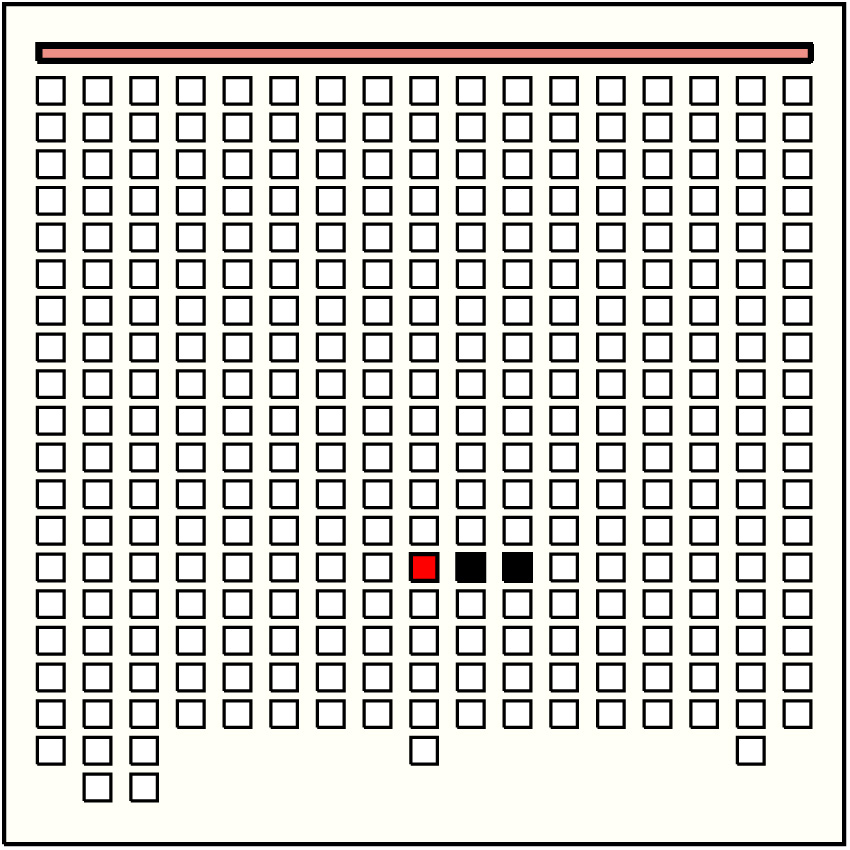
p1639, 14 : 12BD122p182: 2BD + p200: 10BD

Khipu Notes:
Ascher Databook Notes:
  1. By spacing and color patterning, the khipu is separated into 3 parts : part 1 is 3 groups, and parts 2 and 3 are 7 groups each.
    1. Part 1: Assuming that position 10 in group 1 is non-existent, this part consists of 3 groups of 20 pendants each. The color pattern is the same for all 3 groups (with the exception of position 17 in group 3). In all 3 groups, subsidiaries appear only in positions 3, 8,9, 11, 14, 15, 16, 18, 19, 20.
    2. Parts 2 and 3:
      1. Each part is basically 7 groups of 18 pendants. The exceptions of 2 groups with 19 pendants are systematic. The 6th group in each part has an additional W pendant between positions 7 and 8.
      2. Each group in parts 2 and 3 has the same color pattern (with the exception of position 8 in groups 4 and 5 and position 18 in group 4). The color pattern is the same as in part 1 with the systematic difference that positions 5 and 8 of the part 1 pattern do not exist. Thus, there are 18 pendants in each group in parts 2 and 3 as compared to 20 pendants in each group in part 1. Also, while the color in position 19 of the groups in part 1 are B, in parts 2 and 3, the comparable position is BD.
      3. Subsidiaries on pendants in parts 2 and 3 are on a subset of the positions they are on in part 1. Namely, subsidiaries are only on positions comparable to positions 9,15,16,18,20 of part 1.
  2. Many values are uncertain due to breakage. However, we hypothesize that, position by position, values in group 1 of part 1 are related to the sums of values in groups 2 and 3 while values in groups 2 and 3 are related to sums of values in parts 2 and 3 respectively.