AS029/KH0031 - Subsidiary Pendant Sums


Drawings:
Overview Detail View
All Khipus' Ascher Sum FieldmarksRight-Handed XRay
All Subsidiary Pendant Sum RelationshipsLeft-Handed XRay
This Khipu's Fieldmark CatalogSum Overlay
This Khipu's DrawingRight-Handed Sum Detail
Left-Handed Sum Detail

Right Handed Sums:     # Sums = 4,  Max # Summands = 5,   (Min, Mean, Max) Sum Values = (31, 340, 1000)
Click on Image to View Larger


Left Handed Sums:     # Sums = 3,  Max # Summands = 5,   (Min, Mean, Max) Sum Values = (243, 249, 260)
Click on Image to View Larger


Right Handed Sum Detail: - Click on column name to sort
# Color Sum Schema Sum Cord Sum Cord Value # Summands Summands
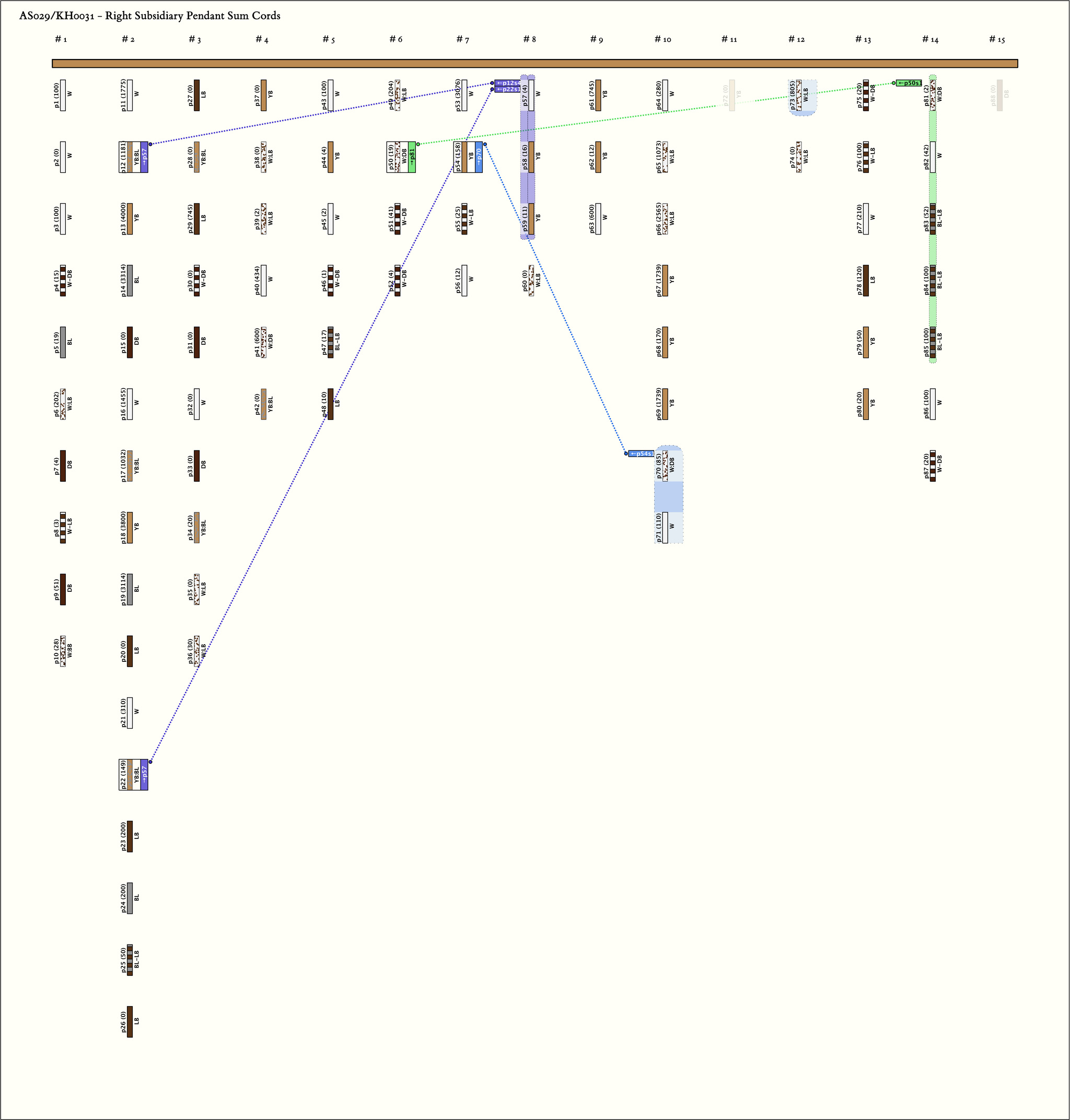
1
p22s12, 12, 1 : 31YB:BL313p57: 4W + p58: 16YB + p59: 11YB
2
p12s42, 2, 4 : 31YB:BL313p57: 4W + p58: 16YB + p59: 11YB
3
p50s16, 2, 1 : 296W-DB2965p81: 2W:DB + p82: 42W + p83: 52BL-LB + p84: 100BL-LB + p85: 100BL-LB
4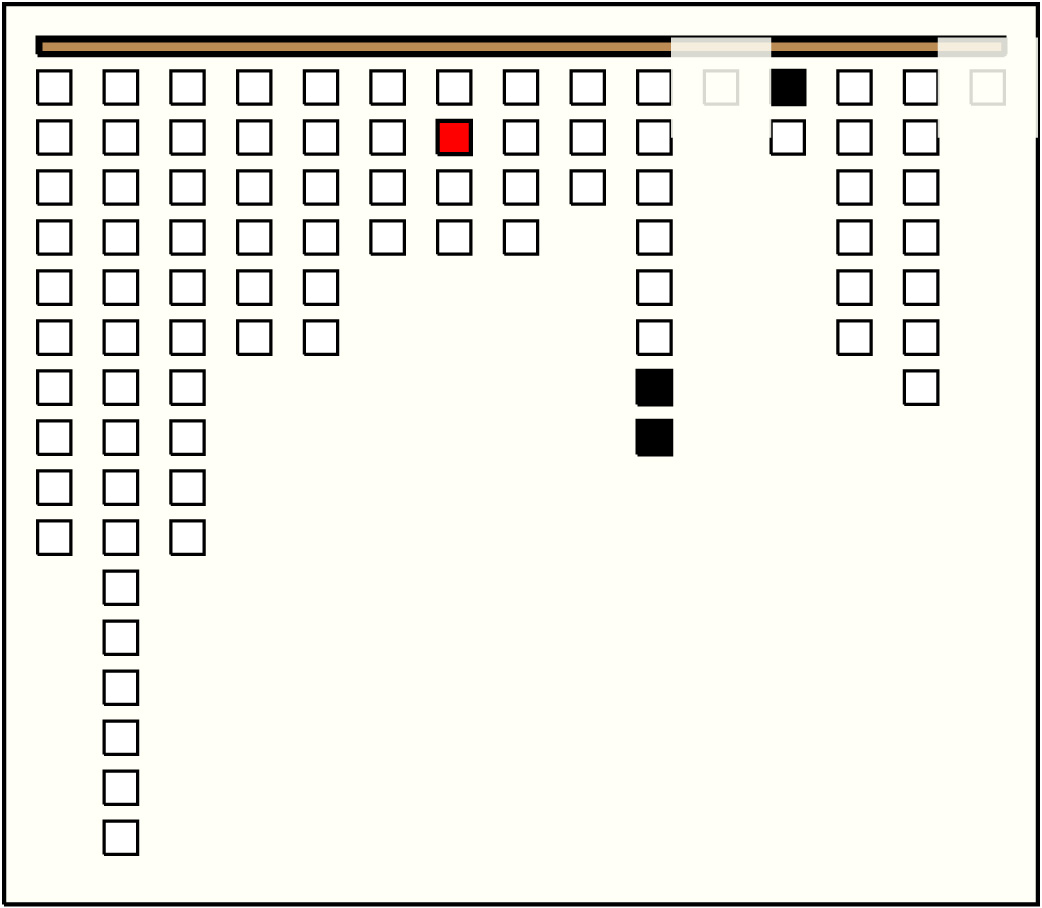
p54s17, 2, 1 : 1000DB10003p70: 85W:DB + p71: 110W + p73: 805W:LB

Left Handed Sum Detail: - Click on column name to sort
# Color Sum Schema Sum Cord Sum Cord Value # Summands Summands
1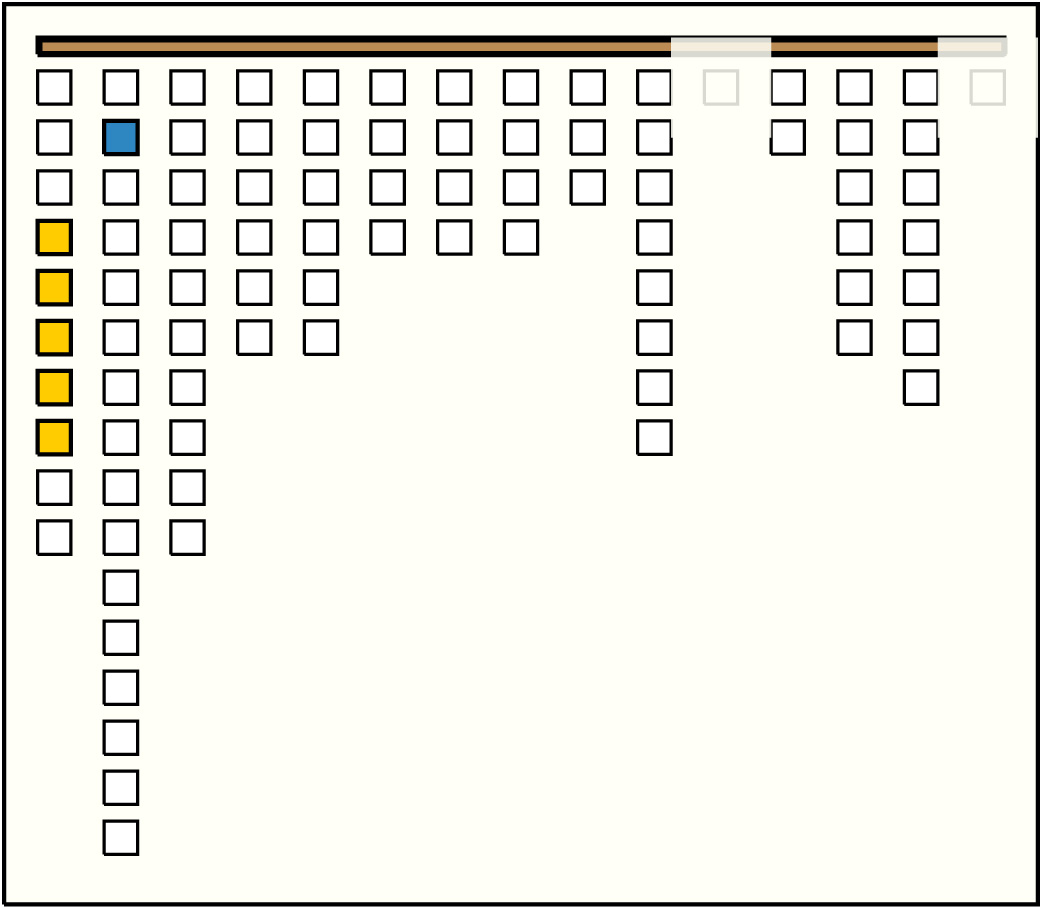
p12s12, 2, 1 : 243BL-DB2435p4: 15W-DB + p5: 19BL + p6: 202W:LB + p7: 4DB + p8: 3W-LB
2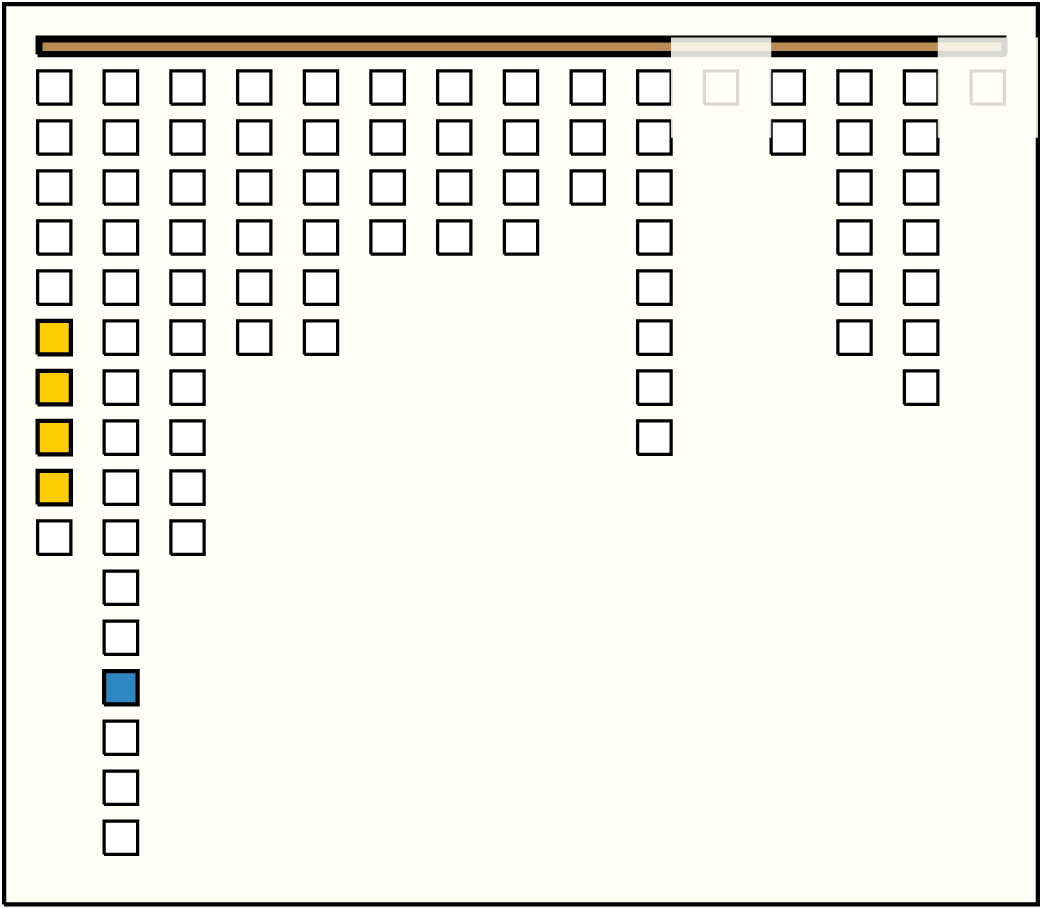
p23s22, 13, 2 : 260W2604p6: 202W:LB + p7: 4DB + p8: 3W-LB + p9: 51DB
3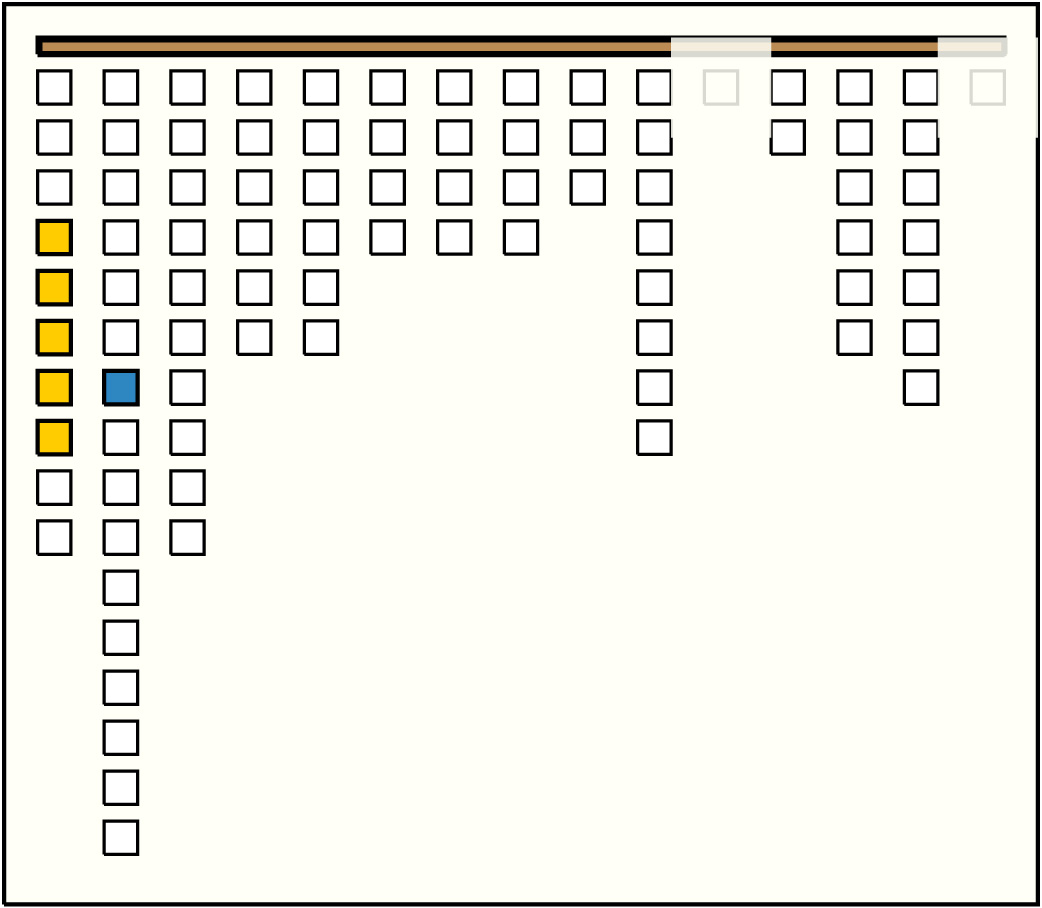
p17s32, 7, 3 : 243BL-DB2435p4: 15W-DB + p5: 19BL + p6: 202W:LB + p7: 4DB + p8: 3W-LB

Khipu Notes:
Ascher Databook Notes:
  1. The end of the pendant cord is formed into a loop 1.0 cm. long.
  2. The pendant cord is mended at 5.5 cm. It appears to have been replaced upside down so the knot order is reversed and was 6s, SL, end knot rather than 1s, SL, 6s. The value would then be 1?65.
  3. The main cord is mended between pendants 71 and 72. Hence, some of the main cord and pendant cords might be missing.
  4. The Museum records the acquisition as Aankoop, July 1956.
  5. Using 6 basic colors, 18 additional cord colors were created. DB appears alone, is twisted with W, is mottled with W, is joined with W in three different orders (DB/W, W/DB/W, DB/W/DB), is twisted with BL, and is joined with BL. The DB-BL twist is joined with W and is joined with DB, while the DB-W twist is twisted again with DB, and the mottled DB:W is joined with DB. LB appears alone, is twisted with W, is joined with W in two different orders (LB/W, W/LB), is twisted with BL and is joined with BL. YB appears alone, is mottled with W, and is mottled with BL. BL and W each appear alone as well as in the combinations described above. BB only appears alone.
  6. By spacing, there are 14 groups varying from 1 pendant to 16 pendants per group.
  7. Groups 1, 2, 5, 6, 8, and 10 have subsidiaries and the other 8 groups do not.
    1. In groups 1 and 6, the subsidiaries always differ in color from the pendants to which they are attached.
    2. In group 1, wherever the pendant value is larger than its subsidiary's value, the difference is the value of another pendant in the group. That is:
      \[P_{i}-P_{i,s1}=P_{j}\;\;for\;(i,j)\;=\;(5,4),\;(7,8),\;(9,10),\;(10,4)\]
      By contrast, in group 8, whenever the pendant value is smaller than its subsidiary' s value, the difference is the value of another pendant in the group. Namely,
      \[P_{i,s1}-P_{i}=P_{j}\;\;for\;(i,j)\;=\;(1,2),\;(2,1),\;(4,1)\]

    1. Five of the 6 pendants in group 5 can be related by summing: P5=P2+P3+P4+P6.
    2. In group 8, 5 of the 8 pendants can be related. The sum of pendants 2 and 3 (which are the same color as each other but different in color from the rest of the group) equals the sum of pendants 4, 5, and 6 (which are the same color as each other but different from the rest of the group).
  9. Group 2 contains 16 pendants with pendants 1-4, 6-9, and 11-14 forming related subgroups within it:
    1. With the exception of P13 which is LB rather than YB, the 3 subgroups repeat the same color pattern (W, YB: BL, YB, BL).
    2. With the exception of a 1 in 1 digit, the first subgroup sums the other two so that
      \[P_{i}=P_{i+5}+P_{i+10}\;\;for\;i=(1,2,3,4) \]
    3. In keeping with its being their sum, Pi has subsidiaries of the same colors and values as Pi+5 and Pi+10 combined. Only one position shows a summation instead : a value of 55+7 appears while the subsidiaries it is adding are 20 and 42. (Of the 32 subsidiaries on the 12 pendants, 3 are not accounted for by this addition.)