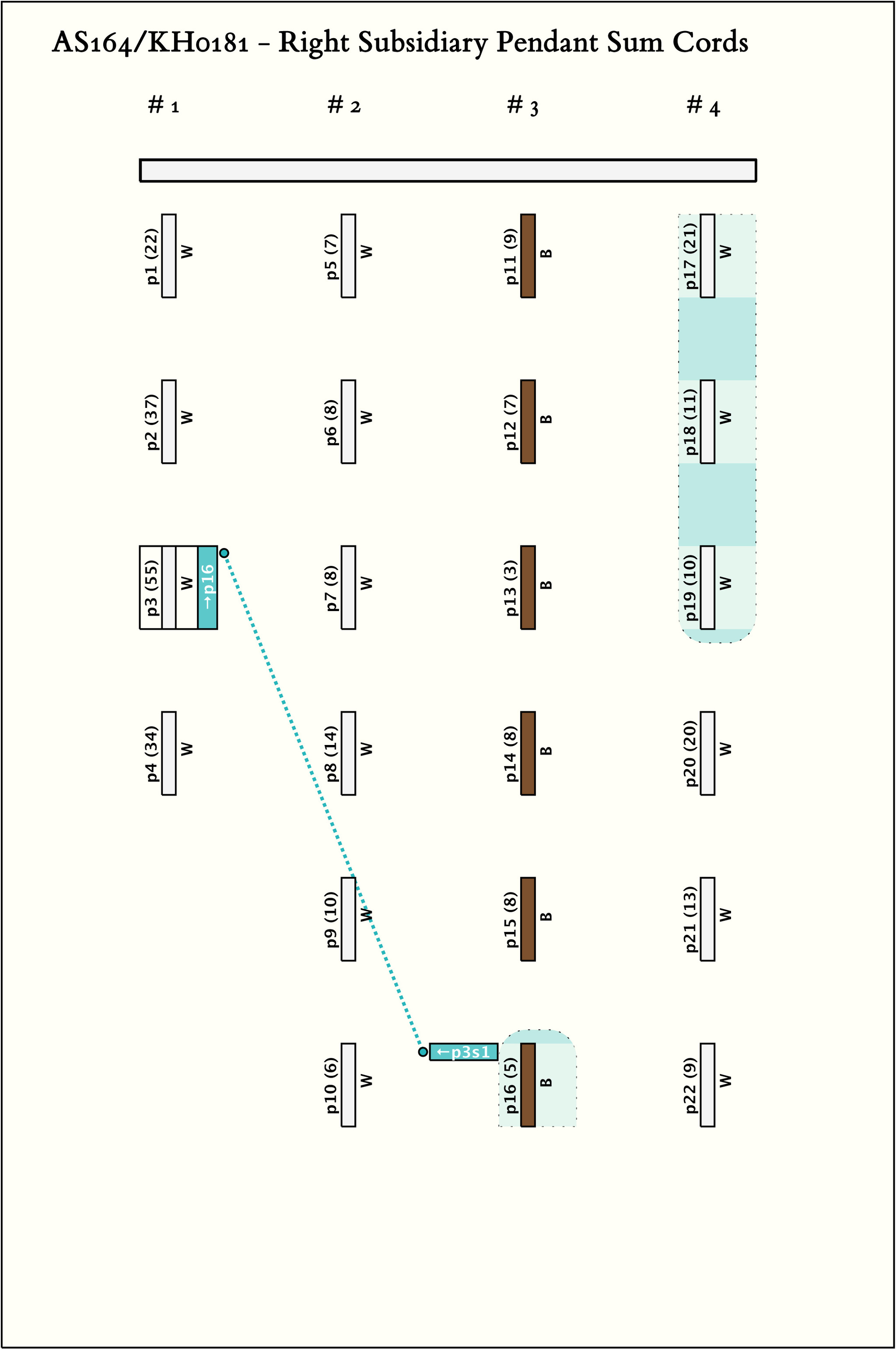
AS164/KH0181 - Subsidiary Pendant Sums
Drawings:
Right Handed Sums: # Sums = 1, Max # Summands = 4, (Min, Mean, Max) Sum Values = (47, 47, 47)
Click on Image to View Larger
Right Handed Sum Detail: - Click on column name to sort
| # | Color | Sum Schema | Sum Cord | Sum Cord Value | # Summands | Summands |
|---|---|---|---|---|---|---|
| 1 |  | p3s11, 3, 1 : 47BS | 47 | 4 | p16: 5B + p17: 21W + p18: 11W + p19: 10W |
Khipu Notes:
Ascher Databook Notes:
- Construction note: The positioning of the knot clusters is not standard. Rather than having all long knot clusters aligned and all single knot clusters aligned, the first knot cluster used is in the highest position. Values have been assigned assuming that the knot cluster positions are "top justified" rather than the usual which is "bottom justified." For example, we usually write numbers "right justified" but can write them "left justified" also. Thus:
541|
23|
47|
left justified
or
|541
|23
|47
right justified - This is one of several khipus acquired by the Museum in 1907 with provenance Ica. For a list of them, see UR1100.
- The positioning of knot clusters discussed in #1 above, is also found on UR1146. (UR1146 has the same Museum acquisition designation.)
- By spacing, the khipu is separated in 4 groups of 4, 6, 6, 6 pendants respectively.
Each group is unified by having all pendants the same color: pendants in groups 1, 2, and 4 are all W; pendants in group 3 are B.
There is one BS subsidiary on each pendant in group 2, no subsidiaries in groups 3 and 4, and 1 or 2 subsidiaries on each pendant in group 1. - Group 1 differs from the other 3 groups by the number of pendants, the varied colors of subsidiaries, and every pendant value is greater than any value in the other 3 groups.
At least 3 of the subsidiary values are sums of values in other groups. Specifically:
\[ P_{11}s1 = \sum\limits_{i=1}^{4} P_{i1} ~~~~~~ P_{14}s1 = \sum\limits_{j=1}^{6} P_{3j} ~~~~~~ P_{14}s2 = \sum\limits_{j=1}^{6} P_{2j}s1 \]